MIST
Magnetosphere, Ionosphere and Solar-Terrestrial
The Broadband Excitation of 3-D Alfvén Resonances (FLRs) in a MHD Waveguide
By Tom Elsden, Department of Mathematics and Statistics, University of St. Andrews, St. Andrews, UK
Field line resonance (FLR) has been the theoretical mechanism used to explain a myriad of ground and spaced based observations of ultra low frequency (ULF) waves in Earth’s magnetosphere. FLR is a plasma physics process whereby energy from a global oscillation (fast mode) can be transferred to local oscillations along magnetic field lines (Alfvén mode), where the fast mode frequency matches the local Alfvén frequency. This process was first studied analytically where the plasma was only inhomogeneous in the radial direction (mathematically 1D) [Southwood, 1974, Chen and Hasegawa, 1974] and has since been extended both analytically and numerically to more complicated systems [e.g. Lee and Lysak, 1989, Chen and Cowley, 1989, Wright and Thompson, 1994, Russell and Wright, 2010].
A feature of FLRs in complicated geometries, such as a dipole, is that the poloidal (radial) and toroidal (azimuthal) Alfvén frequencies are different [e.g. Radoski, 1967]. This infers that the location where the FLR will occur is dependent on the polarisation of the Alfvén wave. This property has recently been explored theoretically in 3D [Wright and Elsden, 2016] and forms the basis of this current work. The magnetosphere is asymmetric and therefore requires an understanding of FLR in 3D. We look at wave coupling in an excessively asymmetric waveguide in order to study the physics clearly.
The figure below taken from Elsden and Wright [2018], displays cuts in the equatorial plane from a 3D MHD waveguide simulation using a 2D dipole magnetic field geometry. In each panel, the x-axis is the radial direction (α) and the y-axis the azimuthal direction (β), and the density varies with azimuth. The left panel shows the energy density (dimensionless units) integrated along a field line, showing an accumulation of energy along curved resonance paths, where the FLR polarisation is between poloidal and toroidal. The middle and right panels show the square root of the kinetic energy in the equatorial plane, revealing ridges which develop by phase mixing in 3D. We find that with a broadband driver it is the natural fast waveguide modes which drive FLRs. Such modes are fairly insensitive to the form of the driver, and hence the resonances are seen at the same locations for many different driving stimuli. This means that the resonances are a property of the medium, and can hence be used as a seismological tool to infer properties of the equilibrium. Finally, the key point is that traditionally FLRs are regarded as having a strictly toroidal polarisation. However, here we have shown in 3D that they can have other polarisations.
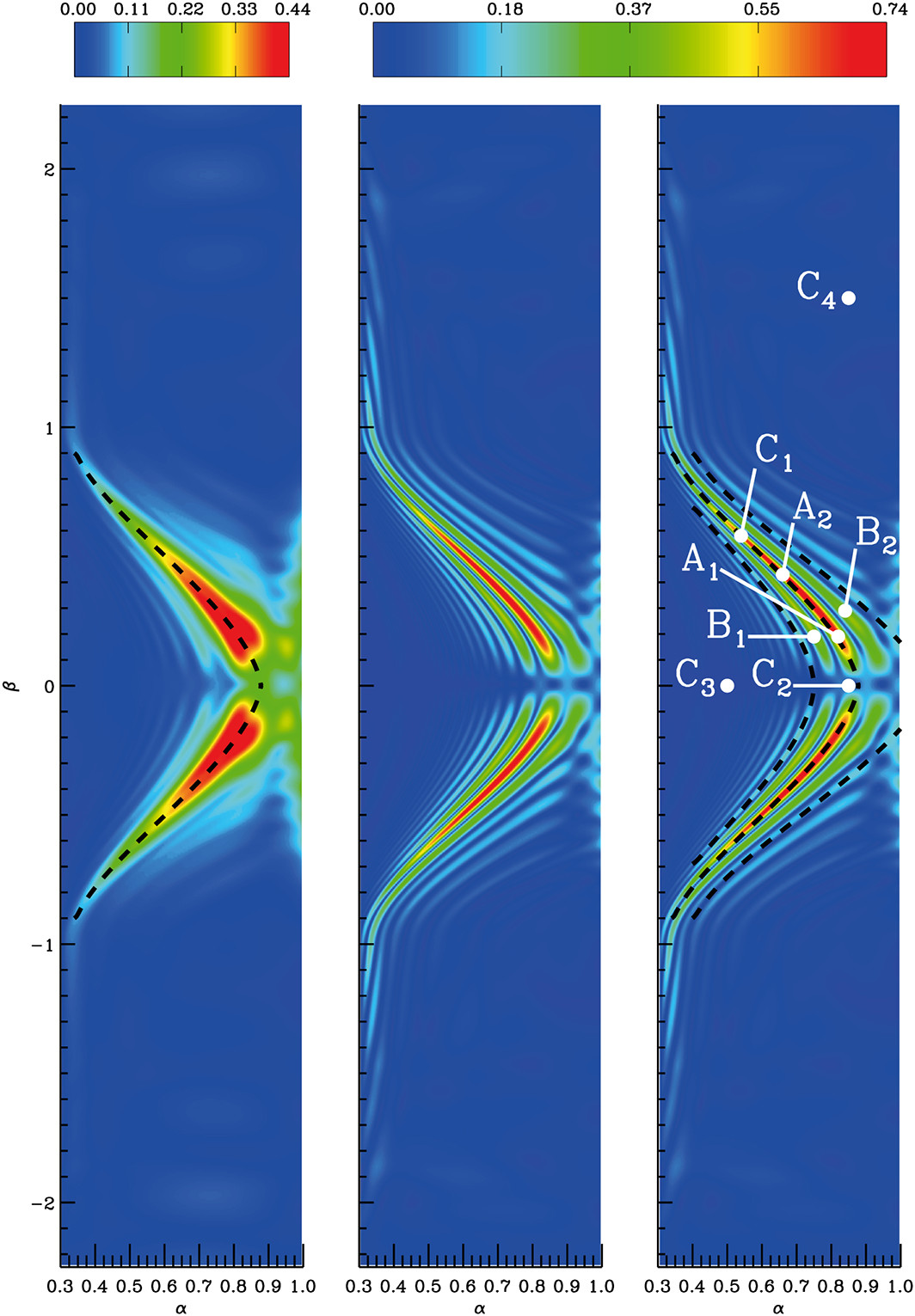
Figure: Left: Energy density integrated along a field line. Black dashed line represents a theoretical prediction of the main FLR location. Middle: Square root of the the kinetic energy in the equatorial plane. Right: Same as middle but annotated for use in other plots in the paper.
